deha magazine / システム開発 / OpenCVのHomographyについての説明
OpenCVのHomographyについての説明
2020/07/06

OpenCVのHomographyは、2つの画像間の画像編集、画像合成、動きの計算、回転、シフトなどを簡単に行う計算方法です。
この記事ではそんなホモグラフィの基本的な計算方法や、実際にOpenCVでどのように書いていけばいいのかなどを紹介しています。
- OpenCVが気になる方
- ホモグラフィについて知りたい方
これらに当てはまる方におすすめの記事となっています。これを読めばホモグラフィの活用方法が分かりますよ。
ホモグラフィとは?
ホモグラフィはオブジェクトプレーンをイメージプレーンにマッピングすることを指します。
ホモグラフィマトリックスは2つの画像間の処理タスクに関連することが多く、2つの画像間の画像編集、画像合成、動きの計算、回転、またはシフトに非常に幅広い用途があります。
計算式は以下の通りです。
HX = sX’
s: 投影の比例定数と0以外
X’: マッピングの結果
X: マッピングされた画像オブジェクト
H:ホモグラフィ行列であり、可逆行列
X ‘からX画像を作成する場合は、ホモグラフィ行列を定義するだけです。
上の本の写真を例に具体的に説明します。
この本2冊で、赤、黄、青、オレンジの4組の点を考慮します。
ホモグラフィは3X3というマトリックスです。
上記の2冊の絵本の対応する点のペアを考えます。たとえば、左が(x1、y1)で右が(x2、y2)の場合、次のようになります。
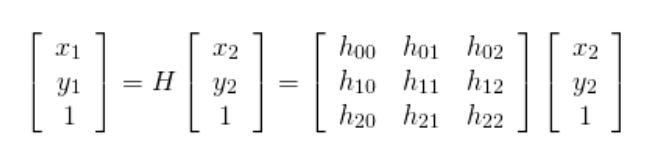
上記の方程式は、2冊の本のすべての対応する点に当てはまります。
したがって、行列Hを取得すると、最初の本の画像を2番目の画像の本の角度に回転できます。
Opencvでホモグラフィ行列を世計算する
2つの画像間のホモグラフィを計算するには、2つの画像間に対応する点の4つが必要です。
Opencvは、すべての点に適合するホモグラフィを推定します。
C++をコードする時、右の本の画像を左の本の画像のように回転する必要があります。
#include “opencv2/opencv.hpp”
using namespace cv;
using namespace std;
int main( int argc, char** argv)
{
//回転が必要な写真を読む
Mat im_src = imread(“book2.jpg”);
// 回転する必要がある本で適当な点の4つ
vector<Point2f> pts_src;
pts_src.push_back(Point2f(141, 131));
pts_src.push_back(Point2f(480, 159));
pts_src.push_back(Point2f(493, 630));
pts_src.push_back(Point2f(64, 601));
// book1の画像を読む
Mat im_dst = imread(“book1.jpg”);
// 回転する必要がある画像で点の4つに該当する点の4つ
vector<Point2f> pts_dst;
pts_dst.push_back(Point2f(318, 256));
pts_dst.push_back(Point2f(534, 372));
pts_dst.push_back(Point2f(316, 670));
pts_dst.push_back(Point2f(73, 473));
//画像の2つのホモグラフィのマトリックスを探す。
Mat h = findHomography(pts_src, pts_dst);
Mat im_out;
//ホモグラフィの通り回転の必要な画像を回転する
warpPerspective(im_src, im_out, h, im_out.size());
// im_src: は回転の必要の画像
// im_out: は結果の画像です。
// h: は以上の計算したホモグラフィです。
// im_out: は結果の画像です。
// im_out.size: 結果画像のサイズです。
//画像の表示
imshow(“Source Image”, im_src);
imshow(“Destination Image”, im_dst);
imshow(“Warped Source Image”, im_out);
waitKey(0);
}
アフィン変換
アフィン変換では、オブジェクトの特徴点を対応する新しい点のセットに変換して、オブジェクト全体に効果を作成します。
たとえば、線の端点のみを使用した座標変換では2つの新しい点が作成され、結合すると新しい線が作成されます。
複雑な変換は、次のような基本的な変換で構成できます。
– 翻訳 (Translation)
– 比率(Scaling)
– 回転 (Rotation)
– 変化 (Shearing)
アフィン変換は2X3 というマトリックスです。
点(x, y) を指定すると、アフィンにより、点 (xt, yt)に変換します。
まとめ
いかがでしたか。本日はホモグラフィ行列をOpencvで行う方法をまとめていきました。
ホモグラフティ行列なら、他のアルゴリズムよりも簡単に画像などを変換することができました。
ぜひこの記事を参考にOpencvでホモグラフィ変換を行ってみて下さい。
dehaでは、5年ほど前から、ベトナムオフショア開発を行っています。
ベトナムでオフショア開発を行う際の費用や、エンジニアの質を知りたい方は、無料で見積もりいたしますので、お気軽にお問い合わせください。



